Long-wave Radiation Heat Transfer
Thermal Radiation Fundamentals
Building surfaces emit thermal radiation by virtue of their absolute temperature. For small surface element (dA) of a Lambertian emitter the radiation flux emitted into a small solid angle (dω) lying in a direction making an angle θ to the surface normal is
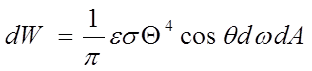
(26)
where
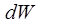
is the radiation flux (W/m
2 )
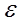
is the surface emissivity (W/m
2 )
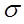
is the Stefan-Boltzmann constant (= 5.6697x10
-8 W/m
2 K
4 )
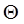
is the absolute temperature of the surface (K)
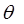
is the direction angle measured from the surface normal
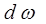
is an element of solid angle
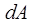
is an element of surface area (m
2 )
Integrated over solid angle, the total radiation (W) emitted by a plane surface of area A is
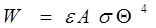
(27)
Surfaces also absorb a proportion of the radiation they intercept. By Kirchhoff’s law the fraction of incident radiation that is absorbed by a surface is equal to its emissivity, ε.
These results represent an idealisation of the physics of radiation emission and absorption in that they assume Lambertian angular characteristics and do not enter into the detail of wavelength dependence (the grey body assumption). However, they provide a sound basis for modelling radiation exchange in buildings.
The emission and absorption of thermal radiation by building surfaces represents an important mechanism for heat transfer. The following discussion centres on the exchange of radiation between solid surfaces. Gases and suspended particales in the air also participate in radiant exchanges and this can be important both inside and outside the building.
Thermal radiation is described as long-wave if it is characteristic of temperatures normally experienced in the human environment. Solar radiation lies in a shorter wavelength band and is treated separately. Surface properties are often significantly different in the long-wave and solar wavelength bands, giving rise to differences between surface emissivity and solar absorptance. Transmission properties are also strongly wavelength dependent: glass is mainly transparent to the solar spectrum but almost opaque in the long wave.
Interior Long-wave Radiation
Radiation heat transfer between a pair of surfaces may be modelled by integrating Equation 26 over emitting area and receiving solid angle. This integration results in a shape factor F 1-2 characterising radiant exchange between the surfaces:
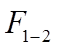
is the fraction of radiation emitted by surface 1 that reaches surface 2
By a reciprocity theorem,
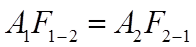
(28)
where A1 and A2 are the areas of surface 1 and surface 2. Each side of this equation represents a radiant exchange area which can be visualised as the portion of surface 1 that effectively radiates all its energy to surface 2 (and vice versa).
By calculating shape factors and accounting for scattering (radiosity), it is possible to construct an accurate model of radiant heat exchange in an enclosure. For practical purposes, however, simpler models are adequate.
Models based on the concept of mean radiant temperature reduce the computational effort involved in radiant exchange calculations by a large factor. Such models introduce a single (fictitious) radiant node which serves as a clearing house for all surface radiant exchange transfers. In an n-surface enclosure this reduces the number of heat transfer pathways from approximately ½ n 2 to n. A variety of mean radiant temperature models have been proposed [ 6 , 7 ]. In all such models the net radiant exchange between a surface and the rest of the enclosure is modelled with an equation of the form
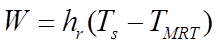
(29)
where

is the net radiative loss from the surface
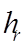
is a surface heat transfer coefficient for exchange with the MRT node
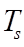
is the surface temperature
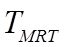
is the Mean Radiant Temperature of the enclosure
The various mean radiant temperature models differ by small amounts in the values assigned to this coefficient. ApacheSim adopts the CIBSE mean radiant temperature model [1], which provides a good representation of radiation exchange where it can be assumed that the emissivities of the surfaces bounding the enclosure do not differ greatly from one another (which is almost always the case).
In the case of holes (openings) between spaces, the holes are treated as highly conducting surfaces with solar transmittance 1 and emissivity 1. The temperature of such a surface will equilibriate at a value near the mean radiant temperature of its surroundings. This temperature will then, in turn, form part of the mean radiant temperature calculations for the adjacent spaces. This approximation has the effect of placing a diffusing medium in the opening.
It will be noted that Equation 29 is a linear function of T s and T MRT . This linearisation of the fourth-power term in Equation 29 forms part of the mean radiant temperature methodology.
The Participation of Air in Interior Radiation Exchanges
Gases present in the air, notably water vapour and to a lesser extent carbon dioxide, participate significantly in radiant exchanges within rooms. These gases radiate to their surroundings by virtue of their absolute temperature and also absorb radiation crossing the space. For these reasons it is meaningful to refer to air emissivity.
The emissivity of the air is mainly due to an infra-red absorption band associated with water vapour. A smaller contribution comes from carbon dioxide absorption.
The water vapour effect increases with humidity and room size, being a function of the product of water vapour pressure and mean path length. For a large room (for example an atrium), the effective air emissivity may be as high as 0.3. For typical rooms such as offices it is usually about 0.1. These values are highly significant. For example the figure for the atrium means that of the long-wave radiation crossing the space, 30% may be absorbed by the air.
The contribution to air emissivity from carbon dioxide is of the order 0.02 for typical CO2 concentrations and can usually be ignored for the purposes of interior radiation exchange calculations.
The most significant effect of air emissivity is its influence on radiant temperature. A radiation-absorbing air mass partially shields warm room surfaces, reducing their effect on the radiant temperature perceived by occupants.
The dependence of air emissivity on humidity also introduces a coupling effect between latent and sensible heat transfers. As the humidity rises, room surfaces exchange more heat with the air and less with each other, and heat sources behave as if their radiant fraction were reduced.
Apache Simulation models the effect of air emissivity due to water vapour. The contribution of carbon dioxide is ignored.
A model of air radiant exchanges was developed by Hottel [10], based on consideration of radiation between a surface and an adjacent hemispherical mass of gas with radius L. For gas masses of other shapes an equivalent mean beam length, L e can be defined. For an enclosure of volume V and surface area A, L e is approximated by
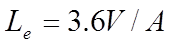
(30)
Hottel’s model expresses the emissivity of the gas as a function of the product p w L e , where p w is the partial vapour pressure of the participating gas. For water vapour, a good approximation to the data at standard atmospheric pressure is provided by the curve fit
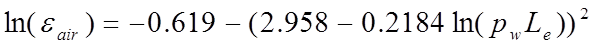
(31)
Air emissivity calculated from equation 31 is used to modify the calculation of the following effects:
Inter-surface radiant exchange
Radiant exchange between surfaces and air
Distribution of radiant plant and casual gains to surfaces and air
Perceived mean radiant temperature
Solar radiation is unaffected by air emissivity, which is effectively transparent to the solar spectrum.
Exterior Long-wave Radiation
Exterior building surfaces receive long-wave radiation from the sky, the ground and other objects in the environment. They also emit thermal radiation. The difference between radiation emitted and radiation absorbed constitutes the net long-wave gain (which in most instances is negative).
The model adopted by ApacheSim for the treatment of exterior long-wave radiation follows work undertaken for the CEC European Solar Radiation Atlas [5], and endorsed by CIBSE in Guide A [1].
The net long-wave gain for an external surface of inclination β (º) is
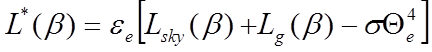
(32)
where
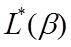
is the net long-wave radiation gain (W/m
2 )
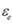
is the emissivity of the external surface
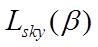
is the long-wave radiation received directly from the sky (W/m
2 )
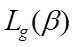
is the long-wave radiation received from the ground (W/m
2 )
is the absolute temperature of the external surface (K)
For a horizontal surface, the long-wave radiation received from the sky is estimated from the temperature and water vapour content of the air, with a modification for cloud cover:
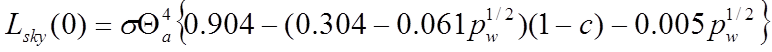
(33)
where
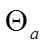
is the external absolute air temperature (K)
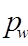
is the external air water vapour pressure (hP)
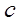
is cloud cover (0-1)
For an inclined surface, the long-wave radiation received directly from the sky is obtained using Cole’s correlation [ 8 ]:
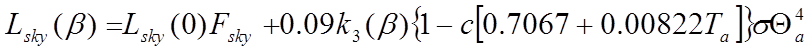
(34)
where
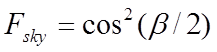
is the shape factor from the surface to the sky

is the external air temperature (ºC)
and
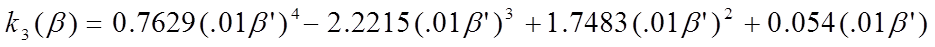
(35)
where
The substitution of β’ for β in the expression for k3 (in contrast to the version of the formula appearing in CIBSE Guide A) avoids unphysical behaviour for slopes greater than 90° (the most important instance of which is exposed floors).
The long-wave radiation received from the ground is estimated from
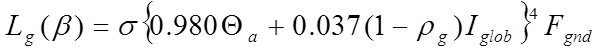
(36)
where
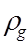
is the (short-wave) ground reflectance (albedo)
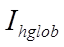
is the total solar flux (W/m
2 ) on the horizontal plane
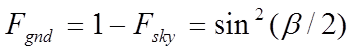
is the shape factor from the surface to the ground
The term involving
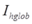
makes allowance for the heating effect of solar radiation on the ground surface temperature.
Where there is diffuse shading from remote objects (as calculated by SunCast) or local shading devices (as specified in APcdb), the long-wave calculations are modified by adjusting the view factors to the sky and the ground using the diffuse sky shading factor:
where
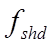
is the diffuse sky shading factor for the surface
The assumption is that the shading objects have a radiosity equal to that of the ground.
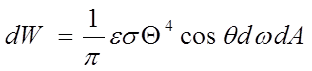 (26)
(26) 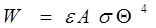 (27)
(27) 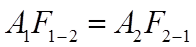 (28)
(28) 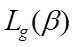 is the long-wave radiation received from the ground (W/m 2 )
is the long-wave radiation received from the ground (W/m 2 ) 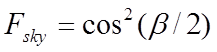 is the shape factor from the surface to the sky
is the shape factor from the surface to the sky 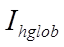 is the total solar flux (W/m 2 ) on the horizontal plane
is the total solar flux (W/m 2 ) on the horizontal plane 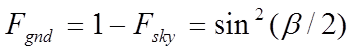 is the shape factor from the surface to the ground
is the shape factor from the surface to the ground 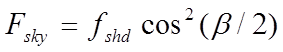
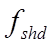 is the diffuse sky shading factor for the surface
is the diffuse sky shading factor for the surface 