Room & Building Heat Balance
ApacheSim uses a stirred tank model of the air in a room. This means that the calculations are based on the concepts of bulk air temperature and humidity, which are assumed to be uniform within the room. If a finer spatial resolution of these variables is required, it can be achieved by subdividing the room, or through the use of computational fluid dynamics (for example MicroFlo).
The task of determining thermal conditions throughout the building proceeds by balancing sensible and latent heat flows entering and leaving each air mass and each building surface. If ApacheHVAC is included in the simulation, the solution process also incorporates thermal balances for each of the system components. If either ApacheHVAC or MacroFlo is included, it also includes the mechanical and natural ventilation air flow rates calculated by these programs, and the inter-dependence between these variables and those calculated within ApacheSim.
Sensible Heat Balance
The balancing of heat flows for the air in each room involves the following components:
· Thermal storage in the air and the furniture (Section 3).
· Convection from the room surfaces (Section 4).
· Heat transfer by air movement (of the three types identified in Section 4.7 ).
· The convective portion of casual gains (Section 8).
· The convective portion of any plant input – idealised (Section 9) or from ApacheHVAC.
By equating the sum of these components to zero, a heat balance is established at the room air node.
Further heat balances are set up for each of the interior room surfaces. The components of the surface heat flow balance are:
· Heat conduction out of the building element (Section 3).
· Convection to the surface from the room air (Section 4).
· Thermal radiation exchanged with the radiant temperature node (Section 6).
· Solar gain absorbed by the surface (Section 7).
· The surface’s share of the radiant portion of casual gains (Section 8).
· The surface’s share of radiant plant input – idealised (Section 9) or from ApacheHVAC.
The use of a mean radiant temperature model of long-wave radiant heat exchange means that a further heat balance is also required at the radiant temperature node, equating all heat flows there to zero.
Finally, there is a heat balance for every exterior surface of the building, involving:
· Heat conduction out of the building element (Section 3).
· Convection to the surface from the outside air (Section 4).
· Thermal radiation exchanged with the external environment (Section 6).
· Solar gain absorbed by the surface (Section 7).
The heat balance equations are solved using linear algebra techniques. Because some of the equations are nonlinear, iteration is used to converge on a global solution.
Latent Heat Balance
The equations dealing with the modelling of air humidity are relatively simple.
A balance of water vapour flows is established for the air in each room, involving:
· Water vapour transfer by air movement (of the three types identified in Section 5).
· The latent portion of casual gains (Section 8).
· The dynamics of water vapour storage in the air (Section 9).
· Any plant humidification or dehumidification – idealised (Section 10) or from ApacheHVAC.
Carbon Dioxide Balance
The modelling of carbon dioxide concentration follows the same pattern as latent heat balance.
A balance of carbon dioxide flows is established for the air in each room, involving:
· Carbon dioxide transfer by air movement (of the three types identified in Section 5).
· The carbon dioxide input associated with People casual gains.
· The dynamics of carbon dioxide storage in the air.
Carbon dioxide transport by air exchange, MacroFlo and ApacheHVAC air flows is modelled by
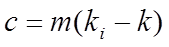
(41)
where
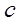
is the carbon dioxide gain (kg/s)

is the carbon dioxide concentration of the supply air (kg/kg)
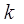
is the carbon dioxide concentration of the room air (kg/kg)
Carbon dioxide inputs to rooms are linked to People casual gains. The sum of the sensible and latent heat inputs from people is taken as an indicator of metabolic output, and linked to carbon dioxide generation in the following way.
The metabolic output associated with different levels of physical activity is measured in MET units. A seated person at rest has an output of 1 MET. This corresponds to a heat output (sensible plus latent) of 58.2 Watts per square metre of body surface. As the metabolic rate increases, heat output rises in proportion. Assuming a body surface area of 1.8 m 2 for an average adult, the metabolic heat output is therefore
Q met = 58.2 x 1.8 M = 104.76 M
where
Q met is metabolic heat output (Watt)
M is metabolic rate (MET).
Carbon dioxide output is also assumed to rise in proportion to metabolic rate, and to take a value of 0.005 l/s (0.3 l/minute) for a metabolic rate of 1.2 MET (a figure corresponding to typical office work):
N = 0.005 M /1.2
where
N = CO2 output (l/s)
Combining these two relations gives CO 2 output as a function of total sensible and latent heat output:
N = 0.005 (Q met /104.76) /1.2 = 3.977x10 -5 Q met
Q met is obtained from the People casual gains data.
The dynamics of carbon dioxide storage in the air are treated in a similar way to the dynamics of moisture storage (see Sections 5 and 9):
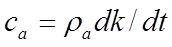
(42)
where
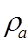
is the air density (kg/m
3 )
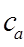
is the net carbon dioxide gain to the air (kg/s)
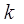
is the room air carbon dioxide concentration (kg/kg)
For reporting purposes, k is converted to a volumetric concentration expressed in parts per million.
If, as a result of a low or zero ventilation rate, the calculated room carbon dioxide concentration rises above 200000 ppm it is capped at this value.
The calculation of room carbon dioxide concentration is based on the assumption that the outside air has a fixed volumetric carbon dioxide concentration of 360 ppm